命題19
2つの相似な立体数の間に2つの比例中項があり、立体数は立体数に対して、対応する辺が対応する辺に対して持つ比の3乗の比をもつ。

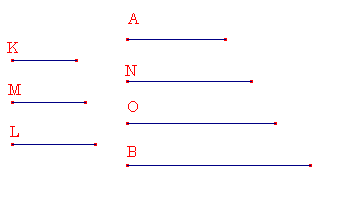
AとBを2つの相似な立体数とし、C、D、EをAの辺とし、F、G、HをBの辺とせよ。
今、相似な立体数は、それらの辺が比例するので、それゆえに、CはDに対して、FはGに対し、また、DはEに対して、GはHに対する。definitionⅦ21
AとBの間に2つの比例中項があり、AはBに対して、CはFに対し、DはGに対し、EはHに対して持つ比の3乗の比をもつと主張する。
CにDをかけてKを作り、FにGをかけてLを作るとせよ。
今、CとDはFとGと同じ比で、KはCとDの積で、LはFとGの積で、KとLは相似な平面数なので、それゆえに、KとLの間に1つの比例中項数Mがある。definitionⅦ21、propositionⅧ18
それゆえに、MはDとFの積で、前の定理の中で証明されていた。propositionⅧ18
今、DはCをかけられてKを作り、FをかけられてMを作るので、それゆえに、CはFに対して、KはMに対する。
しかし、KはMに対して、MはLに対する。
それゆえに、K、M、Lは、CがFに対する比で連続して比例する。propositionⅦ17
そして、CはDに対して、FはGに対するので、いれかえて、それゆえに、CはFに対し、DはGに対する。propositionⅦ13
同じ理由で、DはGに対して、EはHに対する。
いれかえて、K、M、Lは、CがFに対する比、DがGに対する比、また、EはHに対する比で連続して比例する。
次に、EとHにMをかけて、それぞれNとOを作るとせよ。
今、Aは立体数で、CDEはその辺なので、それゆえに、EはCとDの積をかけられてAを作る。
しかし、CとDの積はKである。
それゆえに、EはKをかけられてAを作る。
同じ理由で、HはLをかけられてBを作る。
今、EはKをかけられてAを作り、加えてMをかけられてNを作るので、それゆえに、KはMに対して、AはNに対する。propositionⅦ17
しかし、KはMに対して、CはFに対し、DはGに対し、EはHに対する。
それゆえに、EはHに対して、AはNに対する。
再び、EとHにMをかけられて、それぞれNとOを作るので、それゆえに、EはHに対して、NはOに対する。propositionⅦ18
しかし、EはHに対して、CはFに対し、DはGに対する。
それゆえに、CはFに対して、DはGに対し、EはHに対し、AはNに対し、NはOに対する。
再び、HはMをかけられてOを作り、加えてLをかけられてBを作るので、それゆえに、MはLに対して、OはBに対する。propositionⅦ17
しかし、MはLに対してCはFに対し、DはGに対し、EはHに対する。
それゆえに、CはFに対して、DはGに対し、EはHに対し、OはBに対し、AはNに対し、NはOに対する。
それゆえに、A、N、O、Bは辺の比で連続して比例する。
AはBに対して、対応する辺が対応する辺に対して、つまり、CはFに対し、または、DはGに対し、EはHに対してもつ比の3乗の比をもつと主張する。
今、A、N、O、Bは4つの連続して比例する数なので、それゆえに、AはBに対して、AがNに対してもつ比の3乗の比をもつ。definitionⅤ10
しかし、AはNに対して、CはFに対し、DはGに対し、EはHに対することは証明されていた。
それゆえに、AはBに対して、対応する辺は対応する辺に対して、つまり、CはFに対し、DはGに対し、EはHに対してもつ比の3乗の比をもつ。
それゆえに、2つの相似な立体数の間に2つの比例中項があり、立体数は立体数に対して、対応する辺が対応する辺に対して持つ比の3乗の比をもつ。
証明終了